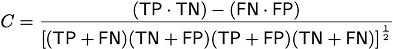RNA Home Aalberts' Lab
Reals: (default: YB donor reals)
Decoys: (default: YB donor decoys)
Auto-validate: (if checked, use same training data to test model; else, cross-validate)
strict PSR (no smoothing, w'=w''=0)
PSR' w':
PSR'' w': w'':
Percent: (percent reduction from using 100 percent of training data)
ROCarea: (reports the area under a Receiver Operating Characteristic curve)
 

To process YB data sets (12623 reals, 269155 falses) takes about 6 sec (PSR), 10 sec (PSR'), 60 sec (PSR'')
A few technical details about our PSR server:
1. Currently, only 7 letter DNA sequences (a,c,g,t) are permitted.
2. The method currently defaults to use the Yeo and Burge real and decoy data sets for human pre-mRNA donor splice sites. (The YB files list the last three bases of the exon and the first four bases of the intron after the conserved GT sequence which is omitted; for example, aagattg is really aagGTattg.)
3. When cross-validating, one-third of the total input data is randomly selected and reserved for testing; the remaining data can be used for training. We have found that it is interesting to study how the performance of the method scales with training data set size --- this reveals whether the method's performance has saturated --- so we allow the user to specify a percentage (0 to 100 percent) of the data to be used for training.
4. The performance measure the program reports is the optimal binary Pearson correlation coefficient between prediction and reality:
,
or the area under a Reciever Operating Characteristic curve (ROC is the True Positive Rate as a function of False Positive Rate).

More on PSR

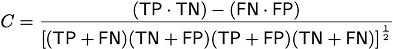A common bioinformatics problem is how to determine whether a local primary sequence X is more like examples in real or decoy training data sets.

Many methods (Weight Matrix Method, Weight Array Method, Markov Models) have been developed to address this problem. A WMM-type approach uses the probabilities of inidividual letters [p(e)>p(t)>...>p(z)] at different positions. Correlations [e.g., qu or th] are included in more sophisticated models.

Our Primary Sequence Ranking methods take a complementary approach, more akin to referring to a dictionary to see whether the word is known. And if the real and decoy dictionaries are small (abridged), we also offer several approaches to enhance the lexicon by making substitution mutations. In the strange world of bioinformatics, local sequence X can appear in both real and decoy dictionaries. (In fact, in our paper we show that in the case of pre-mRNA donor splice signals, 96% of real 7 letter sequences also appear as decoys elsewhere where they are not spliced.)

The PSR approach is very simple. We rank order sequences by the likelihood X is true or '+':

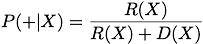
P(+|X) is the number of reals R(X) divided by the total number of occurrances [R(X)+D(X)] of X in real and decoy data sets. This approach selects first the Xs which give the greatest number of reals per decoy. In the limit of infinite training information, the PSR gives the best possible performance. In our paper we show that PSR methods outperform Markov methods for N>50 training data.

To accomodate finite training data, we also provide ways of enhancing the data by including pseudocounts from nearest-neighbor X' and next-nearest-neighbor X'' sequences (one and two substition mutations from X) .


For more details, see our paper.

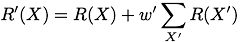
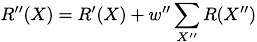
Quantifying Optimal Accuracy of Local Primary Sequence Bioinformatics Methods, Daniel P. Aalberts, Eric G. Daub '04, and Jesse W. Dill '04, Bioinformatics 21, 3347-3351 (2005).